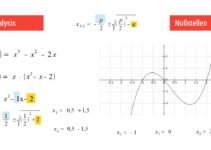
So sieht eine quadratische Funktion aus
Die höchste Potenz gibt den Grad einer Funktion an. Bei einer quadratischen Funktion (Polynom 2. Grades, Funktion 2. Grades) ist die höchste Potenz 2. Der Schnittpunkt der Parabel an der x-Achse heißt Nullstelle. Eine quadratische Funktion hat mindestens zwei Nullstellen.
Quadratfunktion
Eine Funktion \( f , f(x)=x^2\) heißt Quadratfunktion. Die Funktion ist eine nach oben geöffnete Parabel . Ihr Scheitelpunkt liegt im Koordinatenurspung.
Quadratfunktion
Einfluss der Faktoren
Einfluss der Faktor \( a \) \( f(x)=ax^2 \). Ausgehend von \( f(x)=x^2 \). Ist der Faktor negativ, so ist unsere Parabel nach unten geöffnet. Bei \( a>1 \) ist die Parabel gestaucht, sie wird schlanker. Bei \( a<1 \), ist die Parabel gestreckt, sie ist dicker.
Einfluss von Faktor a
Andere Formen einer quadratischen Funktion
Eine quadratische Funktion kann auch einen linearen Anteil und eine Konstante erhalten.
\( f(x)=x^2 +4x -2 \tag{1.1} \)
Quadratische Funktion in Standard Form
\( f(x)=ax^2 +bx +c \tag{1.2} \)
Mit den Faktoren \(a \) und \( b \). Die Funktion besteht aus einem quadratischen Teil, linearen Teil und einer Konstante \( c \)
Quadratische Funktion
Quadratische Funktion faktorisierte Form
\( f(x)=a(x-r_1)(x-r_2) \tag{1.3} \)
Die Nullstellen lassen sich leicht ablesen. \( r_1\) und \( r_2\) sind Nullstellen der Funktion.
Vertex (Scheitelpunkt) Form
\( f(x)= a(x-h)^2 +k \tag{1.4} \)
Der Scheitelpunkt lässt sich ablesen. \( SP(h;k) \)
Scheitelpunkt Form
Weitere Beiträge zu Nullstellen von quadratischen Funktionen
Nullstellen mit der PQ-Formel berechnen!
Nullstellen der Ableitungsfunktion!
Buchtip von mir
Mathematik für Ingenieure und Naturwissenschaftler.