Was muss ich können um diese Aufgabe zu lösen?
Für diese Aufgabe müssen wir ableiten können. Gleichungen ausklammern und Nullstellen bestimmen können.
Gegeben ist die Funktion
\( f(x)=x^3 +4x^2 -2 \tag{1.1} \)
Aufgabenstellung:
- Bestimmen Sie die Hoch- und Tiefpunkte der Funktion \(f(x)\). Ist die Ableitungsfunktion \(f'(x)\) eine nach oben oder unten geöffnete Parabel?
- Bestimmen Sie die Werte der Parameter \(c\), so dass die neue Funktion \(g(x)= f(x)+c\) genau 2 Nullstellen besitzt.
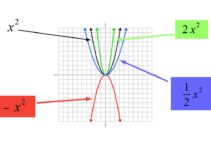
Screenshot aus meinem YouTube Video
Lösungsweg:
Erste Ableitung bestimmen. Aus der 1. Ableitung sehen wir, dass die Parabel nach oben geöffnet ist. Das Vorzeichen bei \(x^2\) bestimmt die Öffnungsrichtung. Ist das Vorzeichen positiv, so ist unsere Parabel nach oben geöffnet. Bei negatives Vorzeichen, nach unten geöffnet. Die Nullstellen der 1. Ableitung sind auch die X-Koordinaten der Hoch- und Tiefpunkte (Extremwert). Die Nullstellen aus\(f'(x)\) in \(f(x)\) einsetzen. Wir haben dann die Koordinaten der Hoch- und Tiefpunkte.
Die Y-Koordinaten der Hoch- und Tiefpunkte entsprechend ist unser Parameter \(c\). Wir haben dann eine neue Funktion \(g(x)= f(x)+c\) mit 2 Nullstellen.
Lösung:
\(g(x)=x^3 +4x^2 \tag{1.2} \)\( h(x)=x^3 +4x^2 – \frac{256}{27} \tag{1.3} \)
Meine anderen Videos zum Thema Nullstellen und Ableitungen?
Nullstellen mit der PQ-Formel berechnen!
Nullstellen bestimmen mit der PQ-Formel
Grundlagen der Differentialrechnung die du brauchst!
Ableitungsregel! Kettenregel, Summenregel, Produktregel usw!