PQ-Formel zum Lösen quadratische Gleichugungen.
Mit Hilfe der PQ-Formel lassen sich quadratische Gleichungen einfach lösen. Der Graph einer quadratischen Funktion ist eine Parabel. Wir bekommen maximal 2 Lösungen \(x_1 , x_2\). Ist der Wert in der Wurzel \(>0\) haben wir eine reelle Lösung. Bei \(<0\) besitz die Lösung einen Imaginärteil.
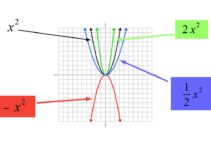
Was ist eine Normalparabel?
Eine Normalparabel ist eine nach oben geöffnete Parabel und ist symetrisch zur Y-Achse. Der Scheitelpunkt liegt im Koordinatenursprrung.
Quadratische Gleichung (Funktion 2. Grades)
\( f(x) = ax^2 + bx + c\tag{1.1} \)
Die PQ-Formel lautet
\( x_{1/2} = – \frac{p}{2} \pm \sqrt{(\frac{p}{2})^2 – q}\tag{1.2} \)
Um die Nullstellen zu bekommen brauchen wir \(f(x) = 0\) und \(x^2\) muss alleine stehen.
\(x^2 + \frac{b}{a}x +\frac{c}{a} =0 \tag{1.3} \)\(p = \frac{b}{a}, q=\frac{c}{a} \tag{1.4} \)
Screenshot aus dem YouTube Video